How to Use

The Combine Operation is a powerful tool designed to merge two graphs into a single, larger graph. This is achieved through the unification of vertices, particularly those with self-loops on the outer face of both graphs.

Getting Started

To utilize the Combine Operation, ensure the following conditions are met:

1. You have two non-simple, non-connected 4-regular graphs. (Note: Self-loops contribute a degree of two to a vertex.)

2. Both graphs have at least one node incident to a self-loop and, in total, at least three vertices on their outer face.

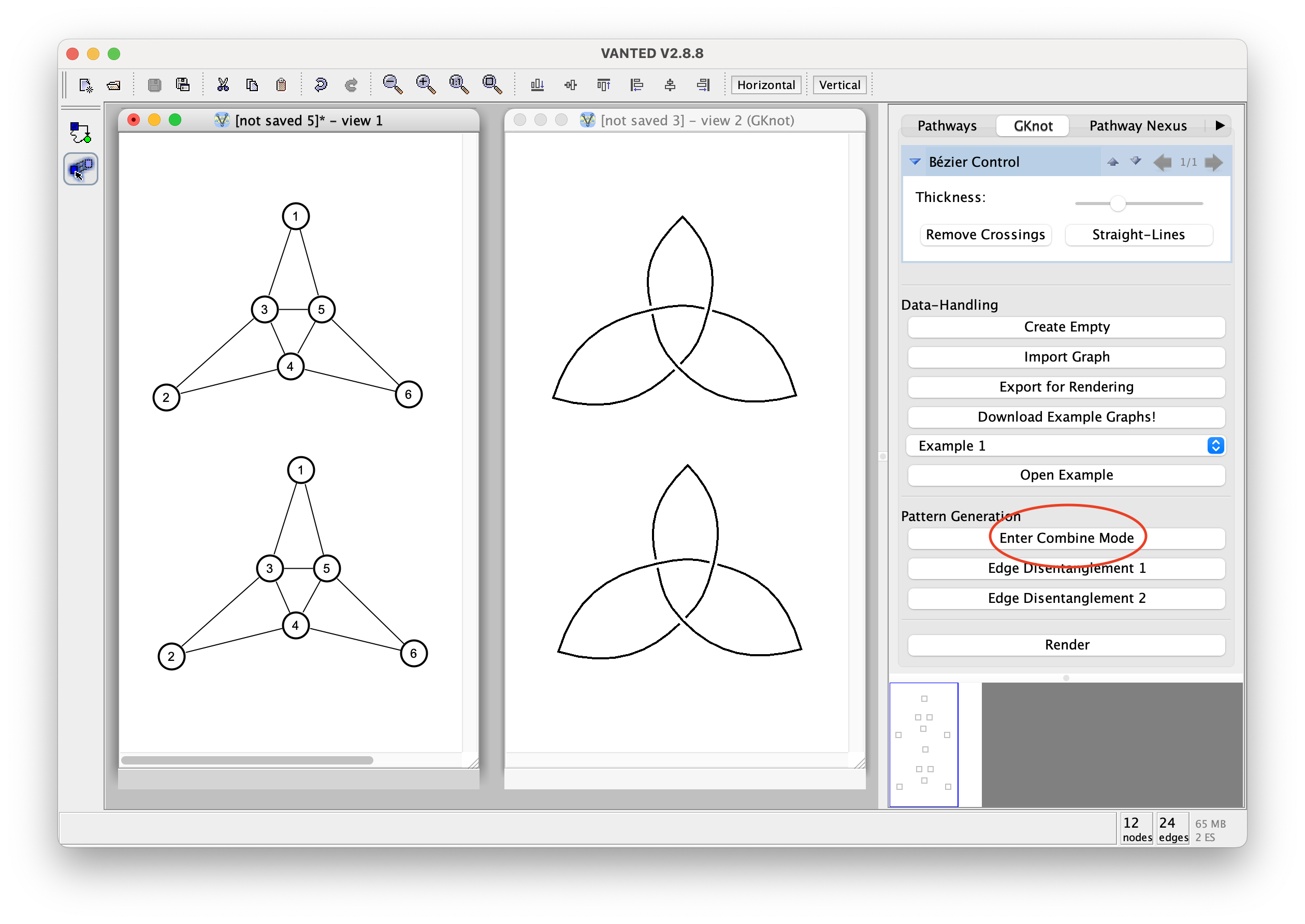
Press 'Enter Combine Mode' to initiate the selection mode for the Combine Operation.

Selection Process

Follow these steps for selecting vertices:

1. First, select the vertices to be combined in the first graph by clicking on any gray vertex. Upon successful selection, the corresponding vertex will turn green.

2. Next, select the subset of vertices in the second graph.

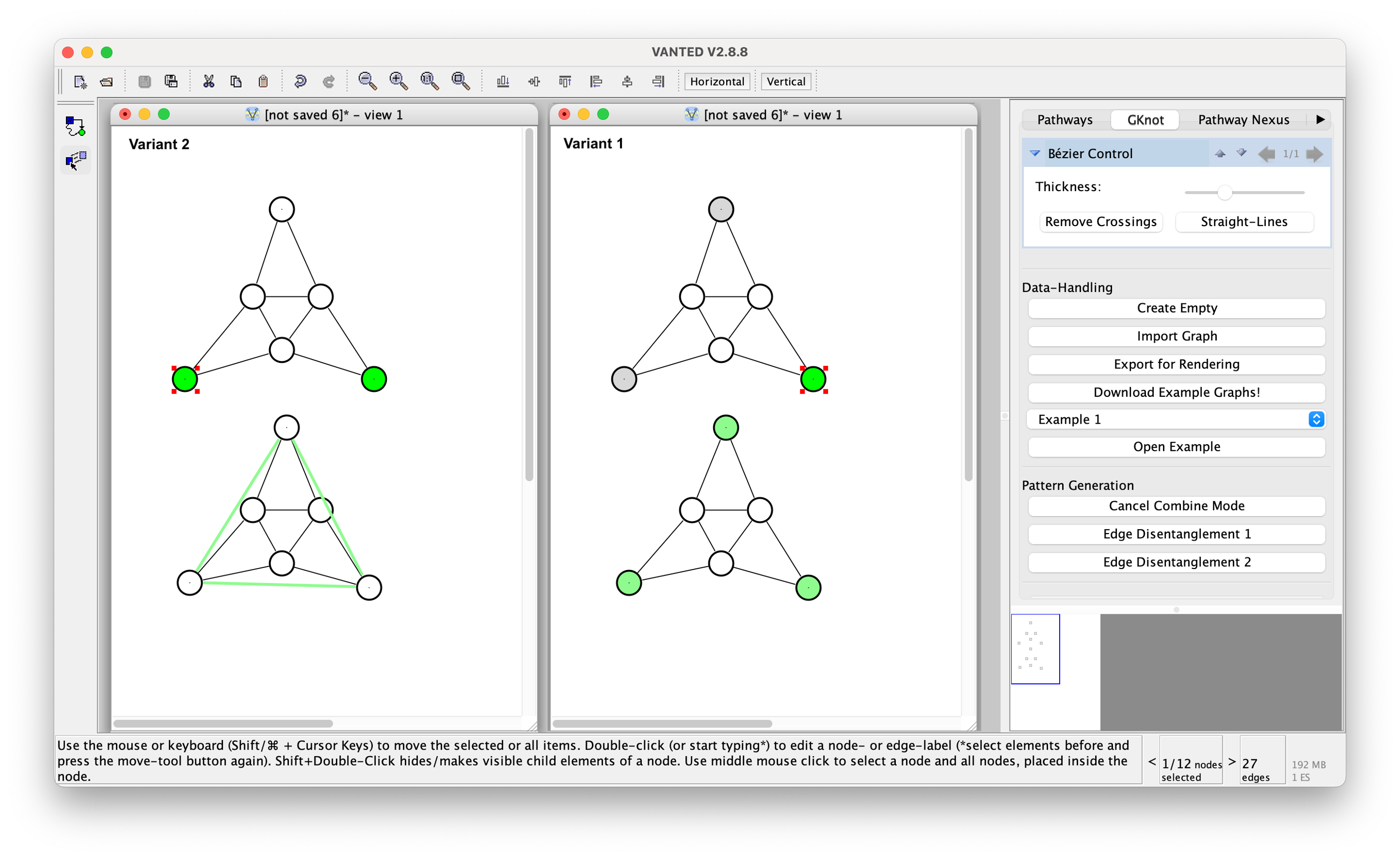
Variant 1: If you selected a single vertex in the first graph, click on any green vertex in the second graph to select a corresponding vertex.

Variant 2: If you selected more than one vertex in the first graph, a green line connecting two or more vertices will appear. Click on this green line to select all vertices that should be combined with the vertices in the first graph.

How to Use

The Edge-Disentanglement Operation is a useful tool to alter the inner structure of a graph, preserving 4-regularity, as well as creating connection points for the Combine Operation.

Edge-Disentanglement 1

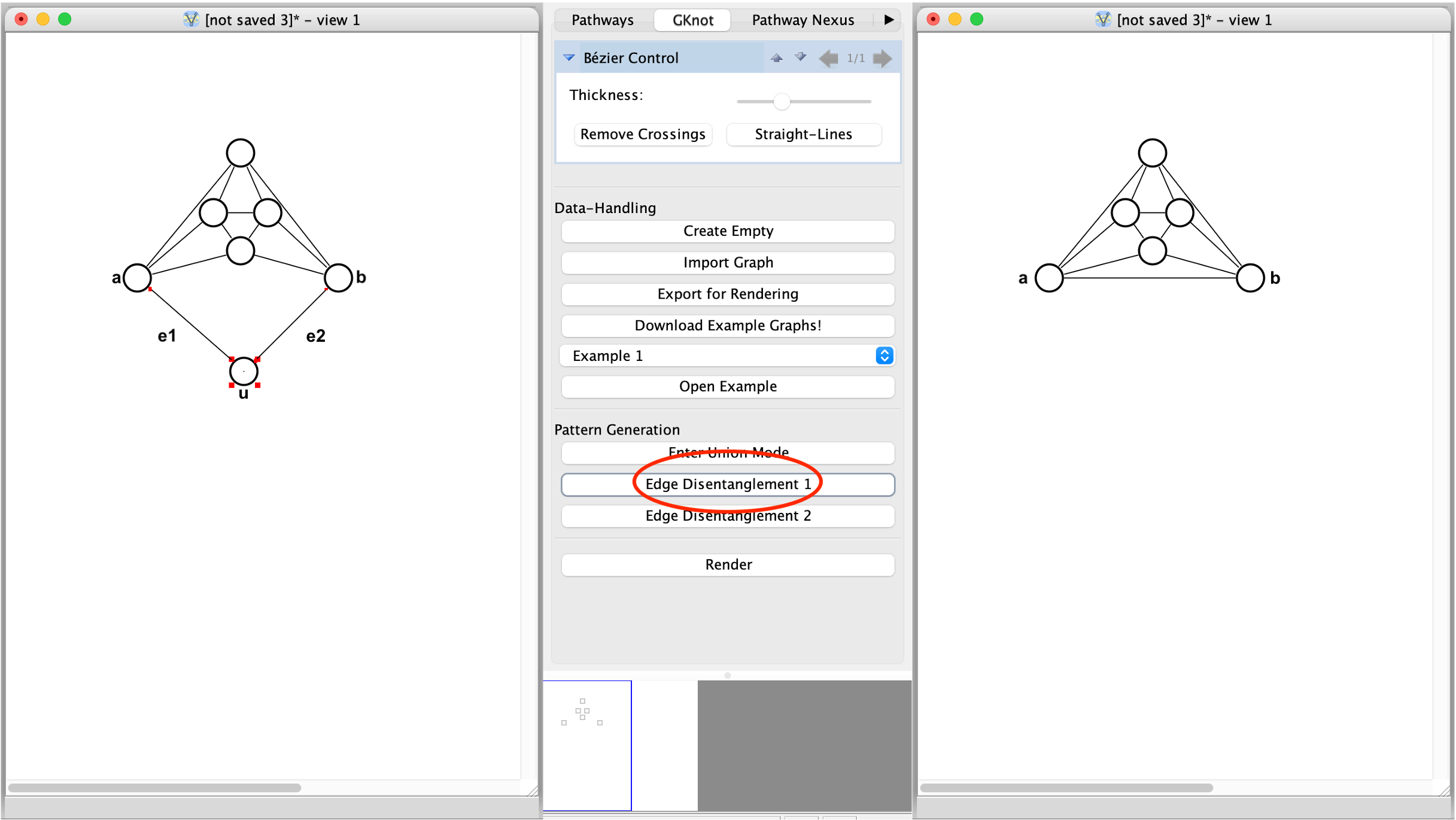
To utilize Edge-Disentanglement Operation 1, select two edges e1 = (a, u), e2 = (b, u) incident to the same vertex u. Depending on the u, we get the following outcomes:

u is incident to a self-loop: u gets deleted, and a new edge e = (a, b) is introduced.



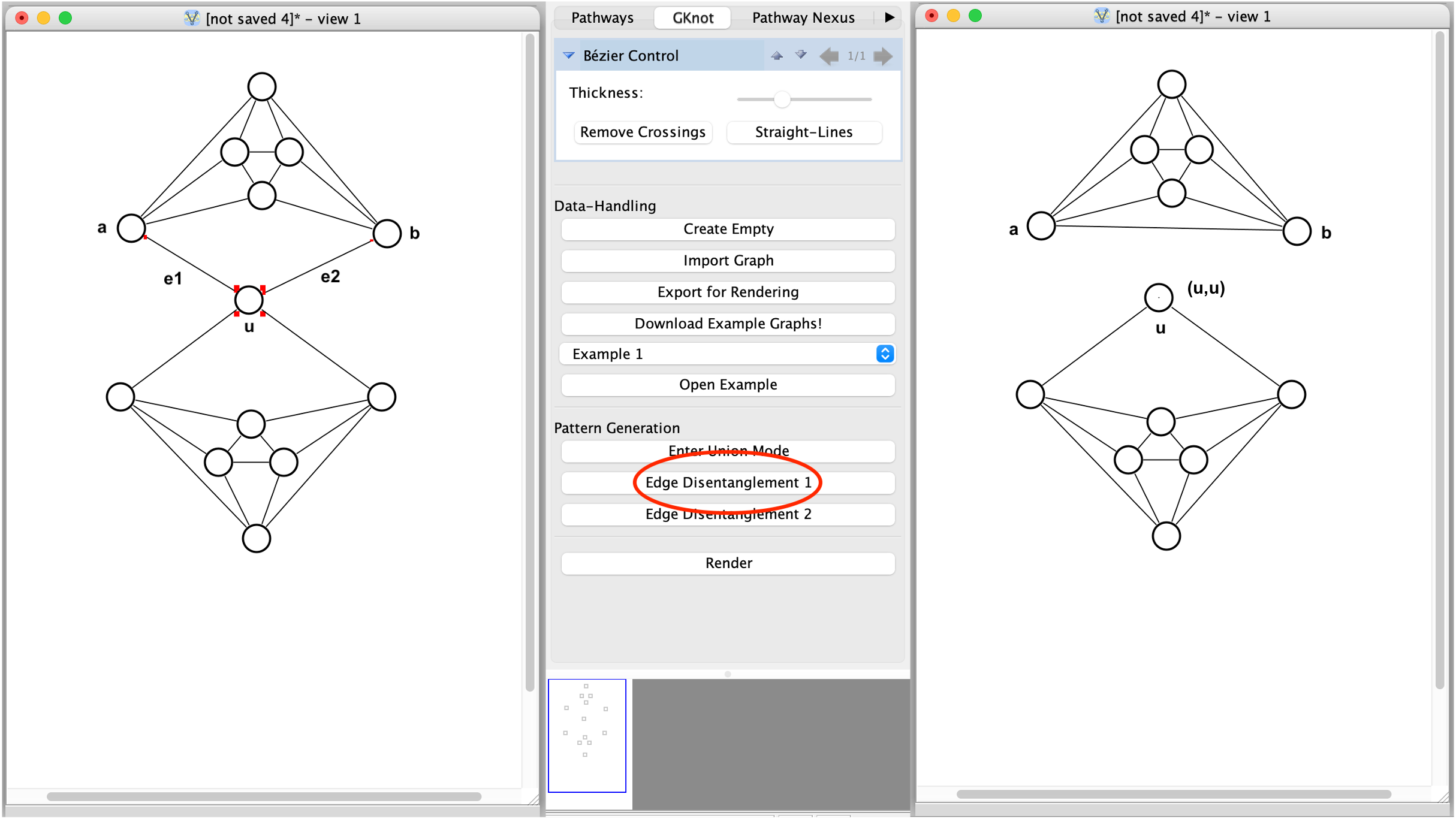
u is not incident to a self-loop: two new edges get introduced - a self-loop (u,u) and a new edge e = (a, b).

Edge-Disentanglement 2

Edge-Disentanglement 2 is the inverse Operation of Edge-Disentanglement 1. Thus, we as well got two cases, depending on what is to be achieved:

Creating a new vertex u: Select an arbitrary edge e = (a, b). A new vertex u incident to a self-loop (u, u) is created. e gets deleted, and two new edges e1 = (a, u), e2 = (b, u) connecting a, b with u get created.



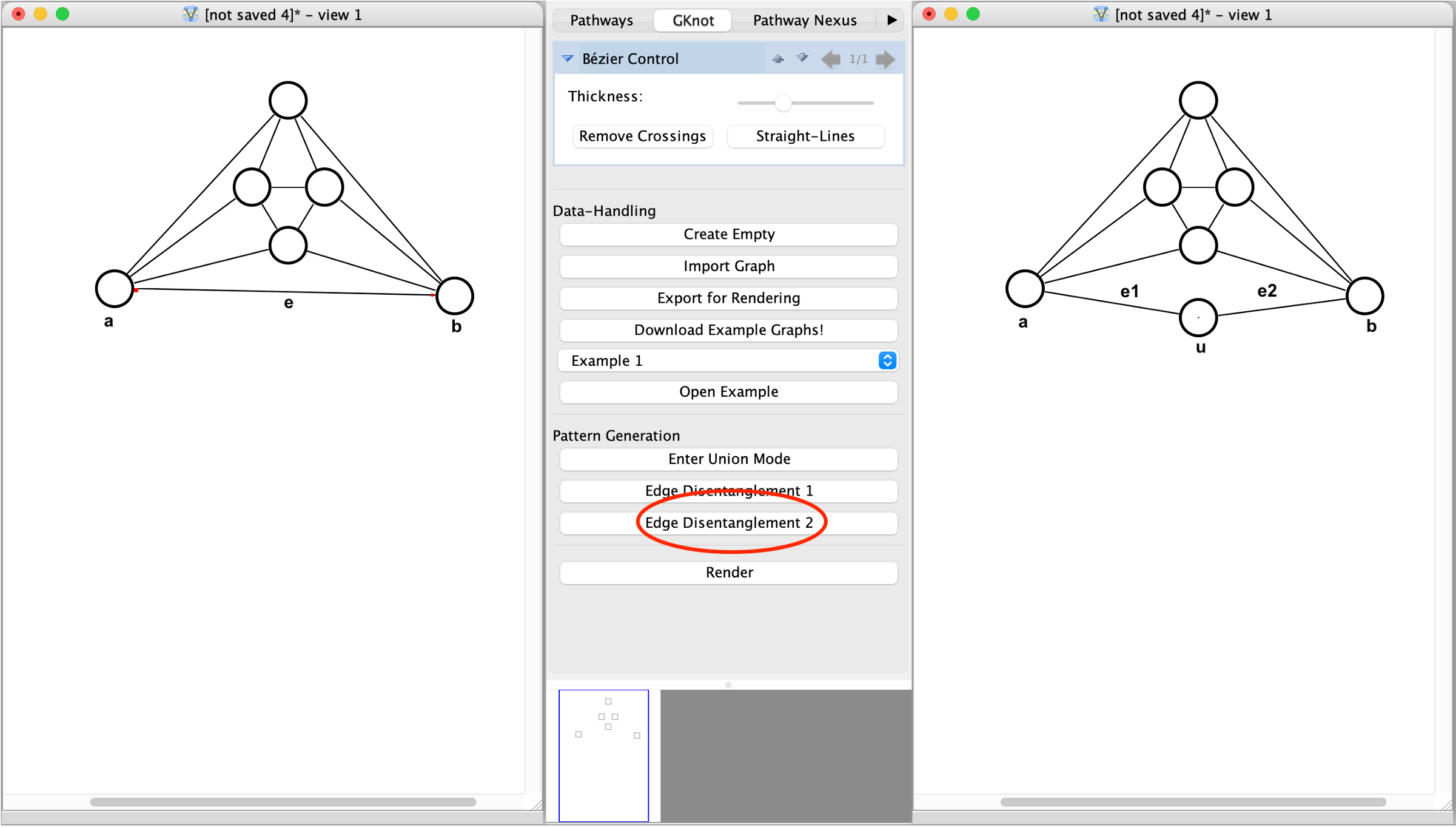
Splitting an edge to a vertex: Select an arbitrary edge e = (a, b) and a vertex u which lies within the same face. e gets deleted, and two new edges e1 = (a, u), e2 = (b, u) get created, connecting both vertices formerly incident to e with u. The self-loop (u, u) gets deleted.